The Busy Beaver, the Placid Platypus and other Crazy Creatures*
James Harland,  School of CS&IT, RMIT
Seminar at CSSE, Melbourne University  16th August, 2005
    *Thanks to Jeanette Holkner, Michael Winikoff and Sandra Uitdenbogerd for assistance with zoological names and descriptions

Introduction
Beaver machines are a particular type of Turing machine:
 Question: For a given number of states, what is the largest number of 1's that can be printed by a beaver machine which halts?

Known busy beavers

      bb(n): maximum number of 1's printed by a terminating beaver machine with n states (often written Σ(n) )
          ff(n): maximum number of state transitions made by a terminating beaver machine with n states (often written S(n))
          prod(M): number of 1's printed by machine M (undefined if M does not halt)

    Hence bb(n) is the maximum value of prod(M) for all n-state machines M.
    Naturally ff(n) ≥ bb(n) and is typically much larger. Possible that the values of bb(n) and ff(n) arise from different machines.

n
 bb(n)
 ff(n)
1 1 1
2 4 6
3 6 21
4 13 107
5 ≥ 4098
 ≥ 47,176,870
6 ≥ 1.29×10865 ≥ 3×101730
7
 ....
 ....

    Consider that a 6-state machine can be represented in 55 bits  ...  (and 10865 takes about 2,800 bits)
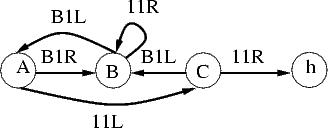
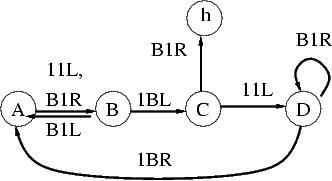
3-state busy beaver 
4-state busy beaver


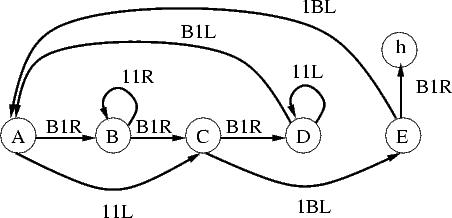
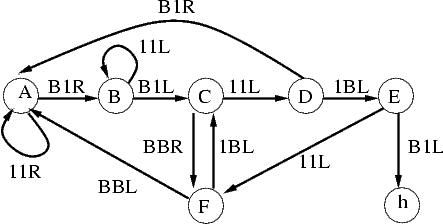
5-state busy beaver candidate 6-state busy beaver candidate



                                 
 

Non-computability

The busy beaver function is non-computable, because it grows faster than any computable function!

Proof: Let f be any computable function.
f computable ⇒ so is F(x)  = Σ 0 ≤ i ≤ x  f(i) + i 2 ⇒ k-state machine MF : x 1's → F(x)  1's

Consider M: X then MF  then MF where X: blank → x 1's. Note X has x states.

M behaves as follows:
 M has x + 2k states ⇒bb(n+2k) ≥ 1's output by M = x + F(x) + F(F(x))

Now F(x) ≥ x 2 > x + 2k for x > m, and F(x) > F(y)  when x > y, and so F(F(x)) > F(x+2k) > f(x+2k)

So bb(x+2k) ≥ x + F(x) + F(F(x)) > F(F(x)) > F(x+2k) > f(x+2k)

Hence, as f was arbitrary, bb is not computable ◊

Green (1964): for any computable f,  f(bb(n)) < bb(n+1)

Hopefully this doesn't apply for n = 5, as otherwise for f(m) =  m m we get
            bb(6) > 4098 4098 ≈ 10 14,804       (!?!?!)

Searching for bb(5) and bb(6) (aka the hunt for the great white whale :-)

How many machines are there?

For n =5 we "only' have to search through 230,400,000,000 = 2.3 ×1011 machines ...

Naive generate and test won't work; the trick is how to incorporate the test into the generation.
Input
 1
 2
 3
 4
 5
B
 O1 = 1, D1 = R, N1 = 2
 not (D3 = R, N3 = 2), N3 ≠ h
 O5, D5, N5 O7, D7, N7 O9, D9, N9
1
 O2, D2, N2
 O4, D4, N4
 O6, D6, N6 O8, D8, N8 O10, D10, N10

Some "global" constraints can be used as well, such as avoiding N3 = 3, D3 = R, N5 = 2, D5 = R.

 Tree normal form:
    
Using equivalences and some other reduction techniques, it seems the number of 5-state candidates is "down" to 69,471,096 ie 6.9 ×107

Loop detection is critical! Mining the data for the 117,440,512 machines with 4 states:

ones
 5
 6
 7
 8
 9
 10
 11
 12
 13
machines
 73,617
 13,029 1981
 475
 79
 13
 6
 5
 2

Preliminary Results for n=5 (or where is the white whale? :-)
Status
 %
halts
 31.9
cycle
 5.2
"growing"
 41.3
blank
 21.5
unclassified
0.1


    Note that classifying 99.9%  of the machines leaves "only" 0.1% or around 65,000 to classify ....
   Work is underway on an inductive prover for non-termination of the form

                        {C}  1N →  {C} 1N+3

Loop checking 
Of course, we may not be able to find all loops automatically, but how close can we get?

Code

Other  Creatures

Revisit first table above

States
 Name
 Final Ones
 Maximum Ones
Hops
 Diagram
3
 bb3
 6
 6
 14
3
 lb3
 6
 6
 11
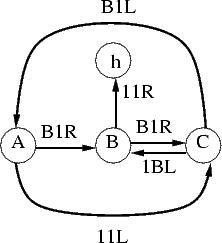3
 ff3
 5
 5
 21
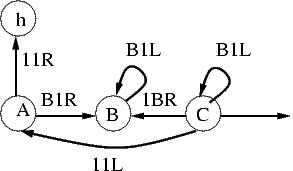4
 bb4
 13
 13
 107
4
 lb4
 13
 13
 96
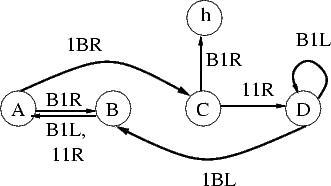5
 m1
 4098
 12,288
 
47,176,870

5
 m2
 4098
   6,144
 
 11,798,826
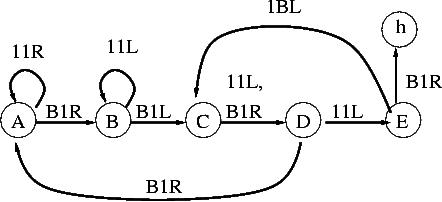5
 m3
 4097
 
 23,554,764

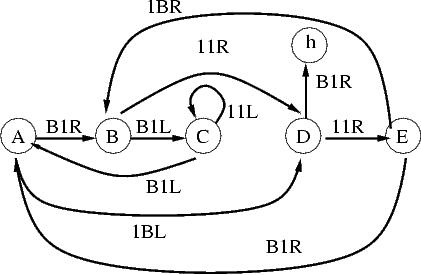5
 m4
 4097
 
11,798,796
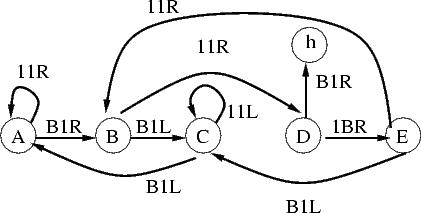5
 m5
 4096
 
11,804,910
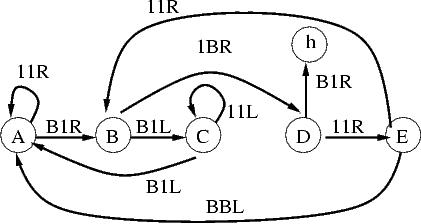5
 m6
 4096
 
11,804,896
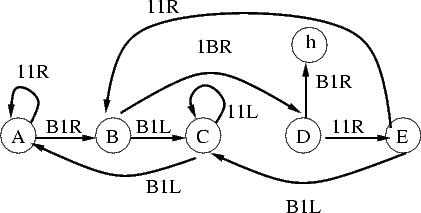5
 m7
 1471
 
  2,358,064

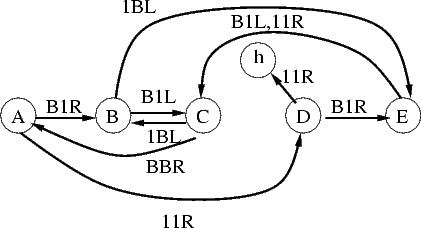6
 ddd
 1.29×10865
3×101730


n-state machine prints m 1's ⇒

Question: what is the minimum number of states needed to print m 1's?

We call this function the placid platypus which we denote by pp(m).

An n-state machine which prints m 1's thus shows that bb(n) ≥  m  and pp(m) ≤ n.
     pp(m): minimum number of states of a terminating beaver machine which prints n 1's
         ww(m): minimum number of state transitions made by a terminating beaver machine which prints n 1's

n
 1
 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
pp(n) 1 2 2 2 3 3 4 4 4 4 4 4 4 5 5 5 5 5 5 5
ww(n) 1 1 5 4 7 11 12 14 19 30 40 53 96 ≤41 ≤45 ≤50 ≤57 ≤63 ≤43 ≤63


n 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
pp(n) 5 5 5 5 5 5 5 5 ? ? 5
 5 5 ? 5 5 ? ? 5 ?
ww(n) ≤72 ≤98 ≤69 ≤223 ≤520 ≤298 ≤343 ≤102 ≤?? ≤?? ≤512 ≤427 ≤559 ≤?? ≤496 ≤494 ≤?? ≤?? ≤856 ≤??

The table below gives the best 5-state machine to print the given number of ones (which coincides with pp(n) for n > 14).
n
 6
 7
 8
 9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
min hops
 8
 12 13
 16
 19
 23
 29
 35
 41
 45
 50
 57
 63
 43
 62
 72
 98
 69
 223
 520
 298
 343
 102
max hops 216 159 276 262 186
 312
 226 349 314
 298 492 420 296 189 611
 419
 642
 855 488
 825
 949
923

n 31 32 33 34 35 36 37 38 39 40
min hops 619 632 559
496 808



max hops 619 632 559
691 808




Not clear that we can fill in every entry in this table.
Question: Is it true that there is a 5-state machine which prints m 1's for each bb(4) ≤ m ≤ bb(5)?

Note that this is certainly false for the range bb(5) to bb(6).
There are at least 10800 numbers to cover, and "only"  (4 × 7)12  = 232,218,265,089,212,416 = 2.3 × 10 17 machines.

So what is the distribution of placid platypus machines?

Equivalence (??)

Consider how one could print 6 1's.
Name
 		States
 		Ones
Hops

4
 		10
 		30

5
 		10
 		26

4
 		12
 		53

5
 		12
 		49
lb3
 3
 6
 11
int4
 4
 6
 9
int5
 5
 6
 8
rr6
 6
 6
 6


     


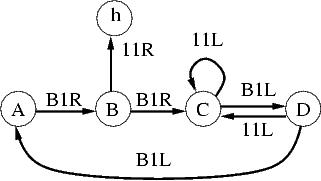
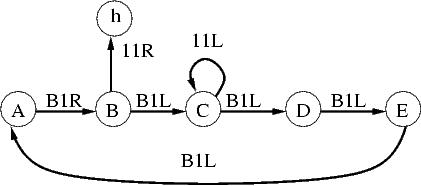
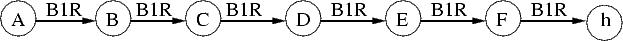
These are all equivalent in some sense. Can we generate the others from the 6-state version?

Mysteries
 To Do List