Animation is a sequence of frames (images), displayed fast enough to appear smoothly changing or continuous.
We have already looked at physically based animation, where objects move according to physics.
Keyframe animation has its origins in traditional hand-drawn animation, where key frames defining the animation would be drawn and then inbetween frames added in a tweening process.
Keyframe animation specifies key values of parameters at key times:

With computers the tweening is performed using interpolation to calculate values.
Keyframe animation is specified using a set of keyframes, i.e. key value and key time (t, v) pairs where t is time and v is the parameter:
Linear interpolation is the simplest type of interpolation: parameter values are calculated in proportion to the difference between key times, i.e. using straight lines.
Sometimes the word lerp is used as shorthand for linear interpolation.
Linear interpolation can be easily calculated using essentially the point-slope equation of a straight line. Given two key frames at (tn, vn) and (tn+1, vn+1)a time t in the interval [tn, tn+1] the corresponding value of v is
v = vn + (t - tn) * (vn+1 - vn) / (tn+1 - tn)
This could be written as
v = vn + (t - tn) * m
where
m = (vn+1 - vn) / (tn+1 - tn)
The interpolation must use the right pair of keyframes, i.e. those whose key times interval [tn, tn+1] contain the time t to be interpolated.
Linear interpolation has problems when used for animation in that motion described by segments of linear interpolation is ``jerky'' and unrealistic. The jerkiness occurs because the rate of change of the parameter being interpolated is discontinous.
Better results are obtained using higher order interpolation using quadratic or cubic equations, also known as splines
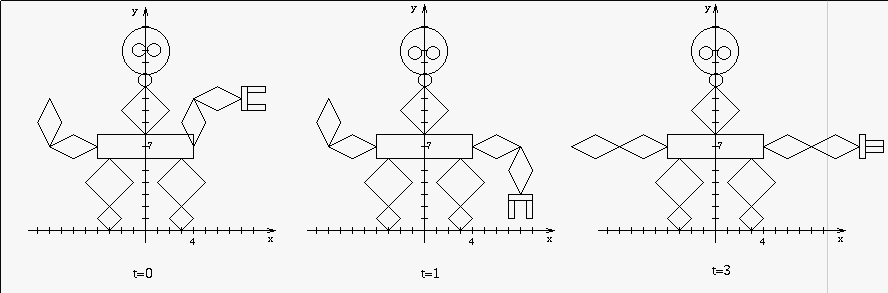
A hierarchical object may be animated using the above techniques.
Parameter curves or motion paths may be specified for each node in the hierarchy.
In a hierarchical object transformations along a branch are concatenated. This means that the transformation given by a parent node will affect its children. Thus the parameter curves or motion paths must be specified with this in mind.
The solar system and flying logo composed of letters are familiar examples of hierarchical animation where individual parts have their own independent motion and the entity as a whole also has motion.
Articulated models are hierarchical models where rigid segments/links/bones are attached to other segments via joints - like the figure above. In articulated models commonly the joints can undergo rotations. In that case the parameters being interpolated are angles.
The approaches to specifying an animation given above, where the animator details the motion which is to occur, is referred to as forward kinematics.
In the forward kinematics approach, to make a robot catch a ball, the animator must specify the motion of the robot and the rotation of each of its joints.
A different approach is {\em inverse kinematics} which is designed to relieve some of the low level tedium.
For articulated objects in some cases it is possible to work out mathematically the transformations which result in a given joint (point) being in a certain place at a certain time. There may be more than one solution.
For instance, it is possible to use inverse kinematics to work out the transformations about a shoulder and an elbow in order that a (fixed) hand be in a certain position. In this case there are two solutions, one with the arm bent up and one with the arm bent down.
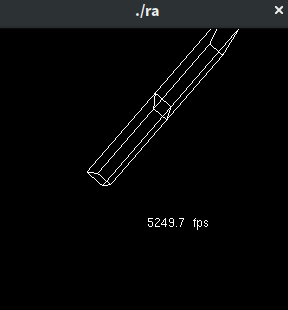
A program which uses key frame animation for the shoulder joint of the Redbook robot arm example