Tutorial: 2D Cannon and Turret - Combining Transformations

The images below show a cannon mounted on a base, i.e. a cannon turret. This is similar to the problem which occurs if a cannon is mounted on a platform which rotates, or the deck of a boat. The tutorial is to go through some steps to be able to aim and fire the cannon, with increasing controls ("degrees of freedom"), including working out the position and direction of the cannon which define the initial position and velocity of the missile.

2D Cannon in the xy Plane

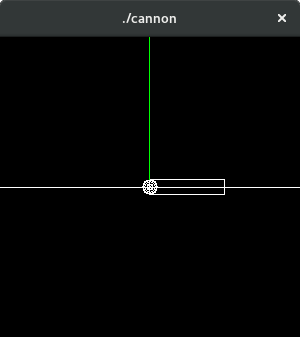
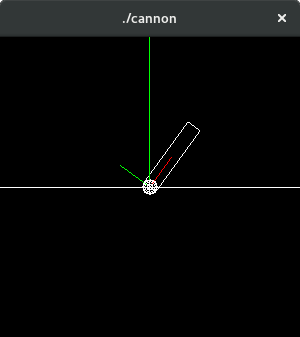
Start by implementing just the cannon rotation. Make the base a line [-1, 1], the cannon a rectangle of length 0.5 and width 0.1. Use wire frame. Allow the turret to rotate around the z axis via an angle α (alpha). Bind the 'a/A' keys for increase/decrease of α by a ±1° increment. When drawing the cannon use glRotate.

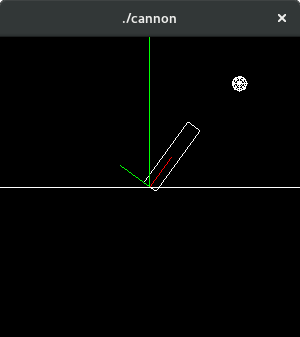
Now add missile firing. Make the missile a sphere of radius 0.05. Remember to convert degrees to radians when calling sin and cos from the C math library, even though OpenGL uses degrees. Write two utility functions degToRad(angle) and radToDeg(angle). Use 'e' to fire the missile, which once fired follows projectile motion (use a low gravity value, e.g. 0.25). Work out the position of the end of the cannon - which is the initial position for the missile, using basic trignometry:

r.x = cannon.length * cos(α)
r.y = cannon.length * sin(α)

The direction of the cannon determines the direction of the missile, i.e. its initial velocity, and is given by essentially the same calculation, but except the velocity vector is obtained by scaling by the missile firing speed:

v.x = missile.fireSpeed * cos(α)
v.y = missile.fireSpeed * sin(α)

Note: use vec2f variables r and v for the position and velocity of the missile, where they are set initially as above. Use numerical integration to move the missile. Set gravity to 0.25.

Adding 2D Turret Base Rotation

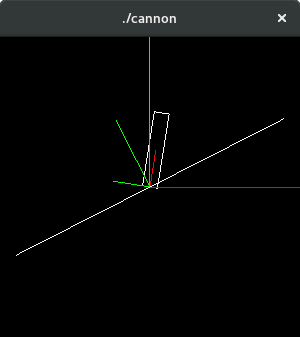
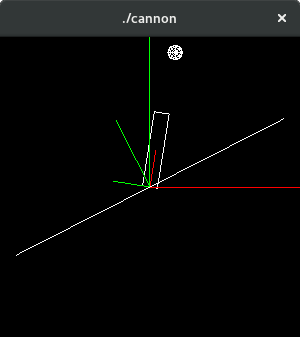
Now assume the cannon is fixed to a turret base which can also rotate around the z axies. Add the ability to rotate the base of the turret around the z axis by the angle β (beta) which also affects the cannon. Use 'b/B' to change β.

Now both angles α and β affect the cannon and missiles. To combine the effect of the two rotations the position of the cannon as worked out above must be rotated by a further amount β. To apply a further rotation around the z axis use the z axis rotation matrix:

$\begin{array}{}\mathrm{P\prime }=RP\\ \left[\begin{array}{}\mathrm{x\prime }\\ \mathrm{y\prime }\end{array}\right]=\left[\begin{array}{cc}\mathrm{cos(\beta )}& \mathrm{-sin(\beta )}\\ \mathrm{sin(\beta )}& \mathrm{cos(\beta )}\end{array}\right]\left[\begin{array}{}x\\ y\end{array}\right]\end{array}$

rr.x = r.x * cos(β) - r.y * sin(β)
rr.y = r.x * sin(β) + r.y * cos(β)
r = rr;

A different variable rr ("rotated r") is used for the rotated position so as to keep the original position which is needed for both x and y calculations (otherwise a bug is introduced). This is now the missile initial position.

The missile initial velocity must also be rotated, using the same calculation.

Now instead of doing the calculations in two steps, where first the cannon is first rotated by α and then β, trying doing the combined rotation by simply adding the angles

r.x = cannon.length * cos(α+β)
r.y = cannon.length * sin(α+β)

and

v.x = missile.fireSpeed * cos(α+β)
v.y = missile.fireSpeed * sin(α+β)